I am going to be working with nichrome wire; so, I thought I would explore some of it’s properties. This is the result.
Summary (TL;DR)
- For a given wire composition and gauge, the steady-state temperature in still air is entirely determined by the current through the wire. In other words, the wire length is irrelevant.
- The resistance of the nichrome wire changes very little with temperature. Its resistance only increases by 7% when changing from 20°C to 400°C; and only increases another 1% from 400°C to 1000°C. The temperature coefficient of resistance of nichrome is much lower than that of most common metals
- The thermal resistance of a straight wire in free still air is NOT constant over temperature.
- For pulse width modulation of either a constant current or constant voltage supply, the temperature rise is approximately proportional to the square of the duty cycle. For example, compared to 100% duty cycle, 50% duty cycle yields 25% temperature rise. This approximation holds true, ±10%, for ΔT < 600°C.
- Due to thermal expansion the nichrome wire will get about 1% longer for every 700°C of temperature rise.
About Nichrome
Nichrome is a metal alloy consisting of primarily nickel and chromium. Varieties of nichrome are available with different proportions of nickel and chromium as well as small amounts of other elements. The more common varieties are nichrome-80 (most common) and nichrome-60 which are approximately 80% and 60% nickel, respectively. Both varieties have maximum operating temperatures of about 1100°C – 1200°C (¹) and melting temperatures above 1400°C (¹). The chromium will form an oxide layer on the wire’s surface which protects the wire from corrosion. The corrosion resistance, the high melting temperature, and a higher resistivity than many other metals makes nichrome a good material for electrical heating elements.
Measuring The Temperature Of The Wire
I could only think of one way to accurately measure the temperature of a wire in free still air that did not depend upon knowing the physical constants that I was trying to measure – a thermal camera, probably requiring a close-up lens. Since I didn’t have one I had to rely on data from wire manufacturers.
References
For this discussion I used data from three companies selling nichrome wire, Omega, WireTronic, and Pelican Wire. The data from the three sources does not entirely agree. Unless otherwise stated, all data is for 30 gauge wire.
Heat It Up With Math
These are the symbols used in the following discussion:
L = length of the wire
ρ = resistivity or resistance per unit length. (This is a constant for any given wire type.)
ρₒ = resistivity of the wire at reference/ambient temperature. (This is a constant for any given wire type.)
α = temperature coefficient of resistance (This is a property of the material.)
R = total resistance of the wire
P = total instantaneous power dissipated by the wire
ΔT = the temperature rise of the wire above ambient temperature, ΔT = T – Tₒ
θ = the radial thermal resistance of the wire to ambient per reciprocal unit length (This is a constant for any given wire type.)
The Fundamental Equations
The resistance of the wire is a function of its length (L) and its resistivity (ρ):
R = ρ * L
The resistivity of the wire (ρ) is a function of its resistivity at ambient temperature (ρₒ), the resistivity temperature coefficient for the wire type (α), and the temperature rise (ΔT):
ρ = ρₒ * (1 + α * ΔT)
The temperature rise of the wire (ΔT) is a function of the power dissipated in the wire (P), the length of the wire (L) and the thermal resistance to the ambient air (θ):
ΔT = P * (θ / L)
Resistance vs. Temperature
Like all conductors nichrome’s resistance varies with its temperature.
The formula for this resistance change is generally given as:
R = Rₒ(1 + α(T-Tₒ))
Where α is the temperature coefficient of resistivity, Rₒ is the resistance at the reference temperature, Tₒ, which is usually 20°C.
The Temperature Coefficient of Resistivity (α)
The temperature coefficient of resistivity represented by the symbol α; defines the change in resistance due to a change in temperature, as per the following formula:
ρ = ρₒ * (1 + α * ΔT)
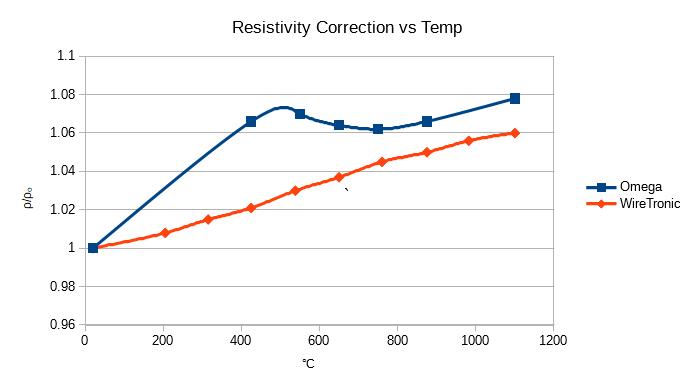
For nichrome, α is often given as a constant ≈ 0.00017 °Cˉ¹. The α for nichrome is much lower than that for most common metals. For example, the α of copper is 24 times that of nichrome. The α for nichrome is not just low relative to other metals; it is a very small value in absolute terms. Even with a temperature change of 1000°C the resistance only increases by 7%. Something that surprised me is that α may not be constant across temperature.
I plotted values for “ρ/ρₒ” versus temperature given by two nichrome wire manufacturers. WireTronic’s data shows a nearly constant value for α across temperature; indicated by ρ/ρₒ being a straight line. But strangely this constant value for α (≈0.00006 °Cˉ¹) is very different from the typically quoted value of 0.00017 °Cˉ¹ for nichrome. Omega’s data shows α changing a lot over temperature; but from 20 °C to 400 °C Omega shows exactly α = 0.00017 °Cˉ¹. It’s a good thing that α is too small to matter much.
The Thermal Resistance of a Straight Wire (θ)
If the thermal resistance of a wire is a constant across temperature, then the temperature rise of the wire should be a linear function of the power dissipated, as per the formula:
ΔT = P * θ
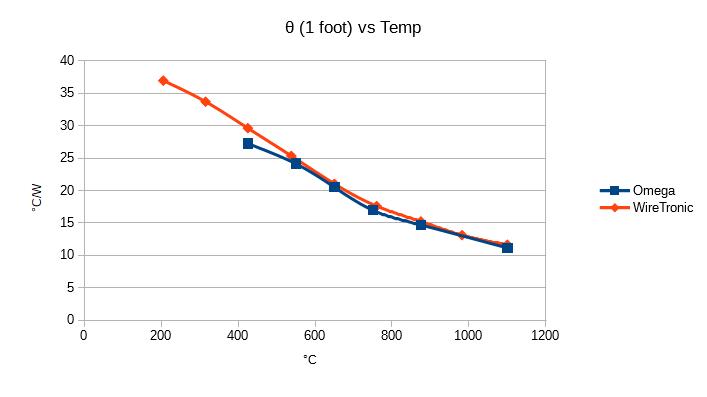
But I used the data from several nichrome wire data sheets to plot θ for a 1 foot long wire.
θ = I^2 * R / ΔT, where R is the resistance of 1 ft of wire at T = Tₒ + ΔT.
Notice how θ varies significantly with temperature. For my purposes I can just treat θ as an unknown constant for any given steady state conditions.
Heating With A Constant Current Supply
Steady-State Current/Temperature Relationship
ΔT = P * (θ / L) [substitute: P = I^2 * R]
ΔT = (I^2 * R) * (θ / L) [substitute: R = ρ * L]
ΔT = (I^2 * (ρ * L)) * (θ / L) [L cancels out]
ΔT = I^2 * ρ * θ [substitute: ρ = ρₒ * (1 + α * ΔT) ]
ΔT = I^2 * (ρₒ * (1 + α * ΔT)) * θ
simplify:
ΔT = I^2 * θ * ρₒ * (1 + α * ΔT)
ΔT = I^2 * θ * ρₒ + I^2 * θ * ρₒ * α * ΔT
ΔT – I^2 * θ * ρₒ * α * ΔT = I^2 * θ * ρₒ
ΔT * (1 – I^2 * θ * ρₒ * α) = I^2 * θ * ρₒ
ΔT = I^2 * θ * ρₒ / (1 – I^2 * θ * ρₒ * α)
Conclusion:
For a constant current source driving a nichrome wire, the properties, θ, α, and ρₒ are independent of the wire length; so, the temperature rise (ΔT) is also independent of the wire length and is only a function of the current (I).
Note: I was dismayed to see that the constant current ΔT equation has a discontinuity at the point where:
I = 1 / √[θ * ρₒ * α]
But otherwise the equation looks reasonable:
a. @ I=0, ΔT=0
b. increasing any of I, α, θ, or ρₒ; increases ΔT
c. the units come out correctly, ΔT=°C and (I^2 * θ * ρₒ * α) = dimensionless
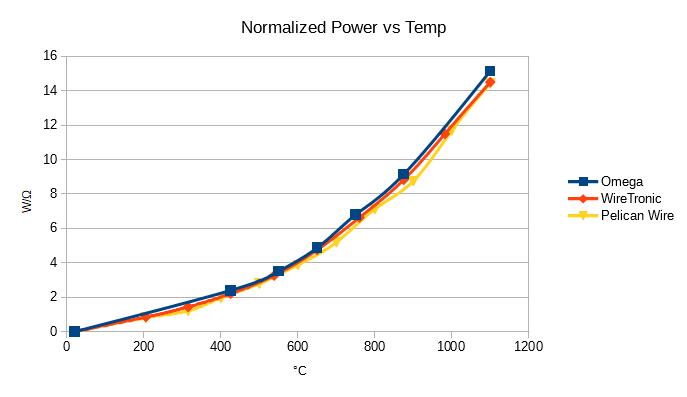
I gathered the current versus temperature data from three sellers of nichrome wire. I plotted the normalized power, Pn = I^2 * ρ / ρₒ, versus temperature. Pelican Wire did not provide data for ρ / ρₒ, so I set it to 1. As you can see from the graph it made almost no difference because α is so small. If α and θ were constants, the graph of normalized power versus temperature would be a straight line – but it is not.
Heating With A Constant Voltage Supply
Steady-State Voltage/Temperature Relationship
ΔT = P * (θ / L) [substitute: P = V^2 / R]
ΔT = (V^2 / R) * (θ / L) [substitute: R = ρ * L]
ΔT = (V^2 / (ρ * L)) * (θ / L) [L does NOT cancel]
ΔT = θ * V^2 / (ρ * L^2) [assume ρ is approx. constant across ΔT]
Conclusion:
The wire’s temperature rise (ΔT) varies with the square of the voltage (V) and varies inversely to the square of the wire length (L). Since θ is also a function of temperature these relationships are not proportional. So for a constant voltage supply, it is difficult to predict the temperature of the wire analytically and repeatibility depends heavily upon matching the length of the wire.
Thermal Expansion
Most materials will expand when their temperatures rise. The amount of this expansion is expressed by the following formula, where α is coefficient of linear thermal expansion.
ΔL = L * α * ΔT
The coefficient of linear thermal expansion for nichrome wire is 14.0E-6. This is an average. The coefficient varies by 5%-10% from 20°C to 1000°C. The wire will get longer as it gets hotter – about 1% longer for every 700°C of temperature rise. If your application requires the wire be stretched tight; it might be a good idea to provide a spring mechanism to compensate for expansion and keep the tension constant.